Vectors is one of the infamous topics that students find trouble with. The questions may seem difficult to approach, and most questions are split into parts, which means that most of the time students are required to complete the first part in order to complete the subsequent parts. However, with a good understanding of vectors and practice, vectors is not as difficult as it seems. In fact, most questions are repetitive as there is only so much that the exam can test.
This article covers the parts that students are usually confused about or afraid of.
Some basics you need to remember in order to tackle challenging questions
- Two vectors a and b are parallel if a = kb for some k ≠ 0
- Magnitude of vector c is denoted by |c|, if c = (x,y,z), then by Pythagoras’ Theorem, |c| = √(x2+y2+z2)
- Three points A, B and C are collinear if (add diagram) for some k ≠ 0
- Unit vector parallel to a, denoted by
- If C is between A and B such that AC : CB = λ : µ, the ratio theorem will give us
- Equation of line:
- Vector form
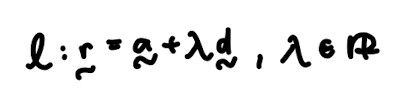
- Cartesian form
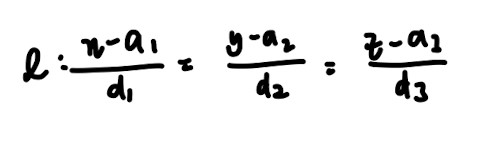
- Equation of plane:
- Vector form
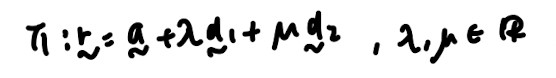
- Cartesian form

- Scalar product form
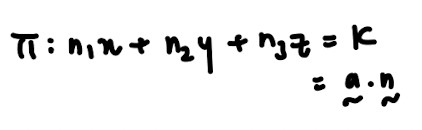
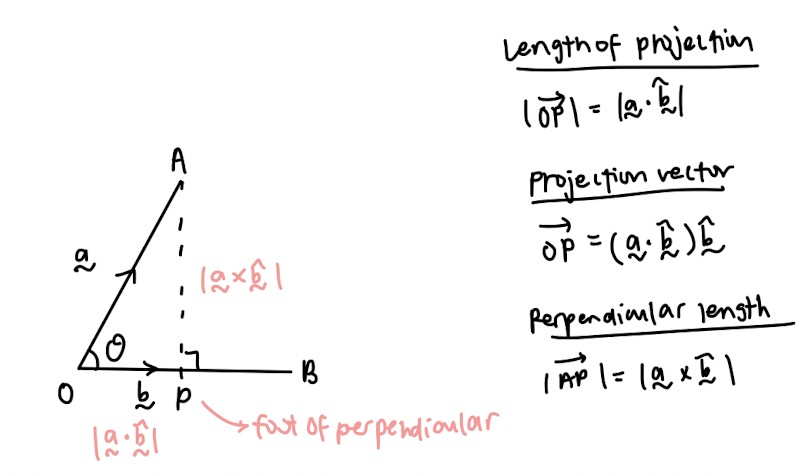
Dot product:
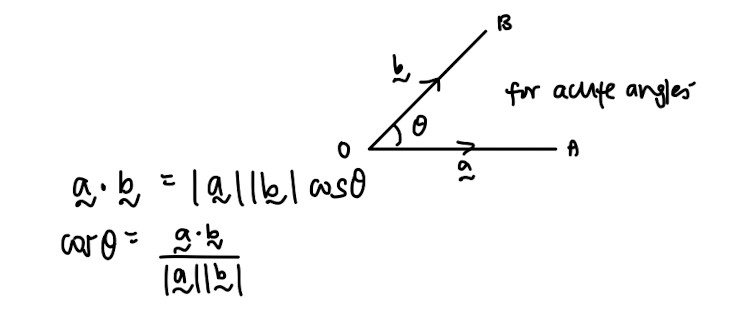
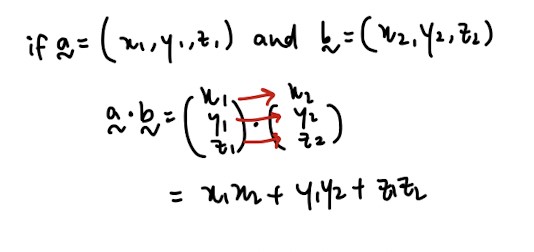
- Important properties that you will need, especially for proofing questions:
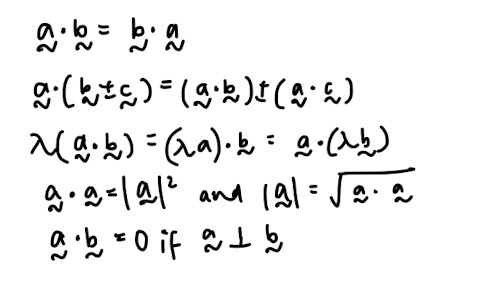
Cross product:
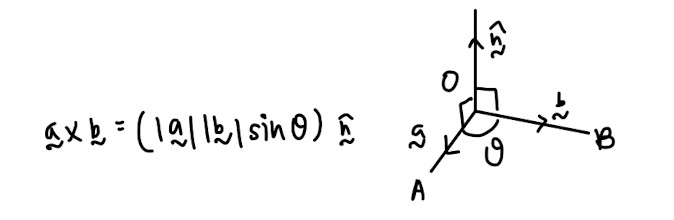
- Important properties that you will need, especially for proofing questions:

Applying your knowledge to commonly tested questions:
- Point of reflection questions – use the ratio theorem to answer this question unless otherwise stated.
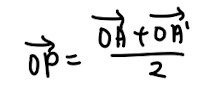
- Questions that ask you to find the line of intersection – Always convert planes to cartesian form first and then solve equations simultaneously using the GC to get the line equation
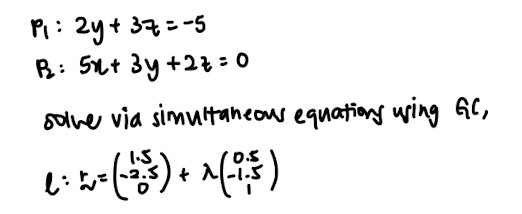
- Prove that they are skew lines
- Show that they are not parallel: d1 ≠ d2
- Show that the lines do not intersect: Solve the simultaneous equations and show that there are no real roots
- Finding distances between point and line, and point and plane
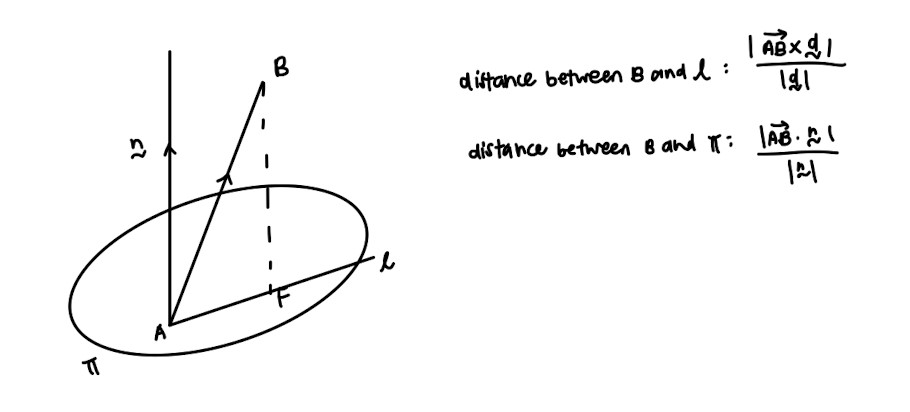
This may seem confusing but when in doubt, always draw the diagram for a better understanding of the question. It will not take that much time!
- Finding angles
- Angle between ℓ1 and ℓ2: d1 d2 = |d1||d2| cos θ
- Angle between ℓ and π: d n = |d||n| sin θ
- Angle between π1 and π2: n1 n2 = |n1||n2| cos θ
- Direction cosines (not always tested, but just in case they test it)
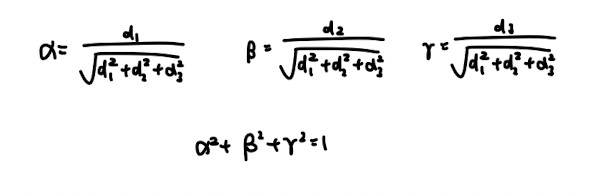
direction cosines
Final words of advice
Questions may be confusing at times, but don’t panic, draw out the diagram and recall the basic dot and cross product. Thus, this requires you to have a solid understanding of dot and cross products and when they are used. Do as many revision questions as possible, and you will realise that vectors questions are actually very repetitive.
If you need any help with H2 Maths – Vectors or other maths topics, our professional and very experienced tutors are always available to help.

